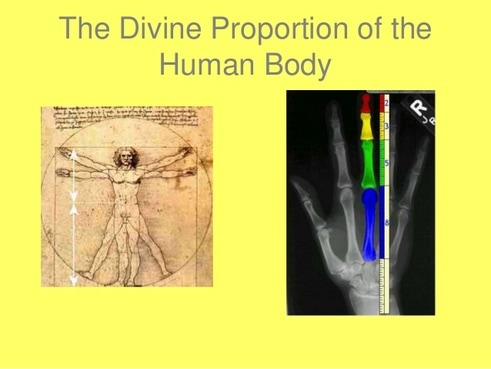
🌸
The Fibonacci Sequence
🌸
The Fibonacci Sequence
🌸
🌸
What is the Golden Ratio?
What is the Golden Ratio?
🌸
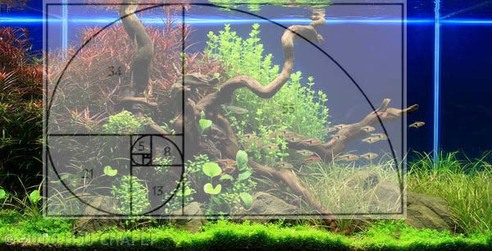
If we look at the sunflower, we will see the spiral shape.
It is exactly 21 or 34, depending which direction we look .
🌸
If we look at the sunflower, we will see the spiral shape.
It is exactly 21 or 34, depending which direction we look .
🌸
🌸
The Golden Number
Approximately
1.618 033 988 749 894 848
🌸
The Golden Number
Approximately
1.618 033 988 749 894 848
🌸
🌸
Drawing of Hemchandra Based on Vikram Samvat 1294 Palm Leaf
The Golden Ratio Was Dicovered
in 1150 and described by two Indian mathematics
Gopala and Hemacsandra who examined the theoretical aspects of the Sanskrit prosody.[ 8][13]
Susantha Goonatilake writes that the development of the Fibonacci sequence
"is attributed in part to Pingala (200 BC), later being associated with Virahanka (c. 700 AD),
Gopāla (c. 1135), and Hemachandra (c. 1150)".[7]
However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):
The sequence is also discussed by Gopala (before 1135 AD) and by the Jain
scholar Hemachandra (c. 1150).
🌸
in 1150 and described by two Indian mathematics
Gopala and Hemacsandra who examined the theoretical aspects of the Sanskrit prosody.[ 8][13]
Susantha Goonatilake writes that the development of the Fibonacci sequence
"is attributed in part to Pingala (200 BC), later being associated with Virahanka (c. 700 AD),
Gopāla (c. 1135), and Hemachandra (c. 1150)".[7]
However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):
The sequence is also discussed by Gopala (before 1135 AD) and by the Jain
scholar Hemachandra (c. 1150).
🌸
Golden Ratio
Fibonacci Numbers
The golden ratio, geometric ratios, and geometric figures were often employed in the design of Egyptian, ancient Indian, Greek and Roman architecture.
Medieval European cathedrals also incorporated symbolic geometry. Indian and Himalayan spiritual communities often constructed temples and fortifications on design plans of mandala and yantra. For examples of sacred geometry in art and architecture refer:
Labyrinth (an Eulerian path, as distinct from a maze) Mandala – Parthenon -Taijitu (Yin-Yang) - Tree of Life - Rose Window Celtic art such as the Book of Kells – Yantra - Dharmacakra
The golden ratio, also known as the gold ratio, golden proportion, golden mean, golden section, golden number, divine proportion or sectio divina, is an irrational number, approximately 1.618 033 988 749 894 848, that possesses many interesting properties.
Shapes proportioned according to the golden ratio have long been considered aesthetically pleasing in Western cultures, and the golden ratio is still used frequently in art and design, suggesting a natural balance between symmetry and asymmetry.
The ancient Pythagoreans, who defined numbers as expressions of ratios (and not as units as is common today), believed that reality is numerical and that the golden ratio expressed an underlying truth about existence.
Since the Renaissance, many artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing.
Mathematicians have studied the golden ratio because of its unique and interesting properties.
🌸
Fibonacci Numbers
The golden ratio, geometric ratios, and geometric figures were often employed in the design of Egyptian, ancient Indian, Greek and Roman architecture.
Medieval European cathedrals also incorporated symbolic geometry. Indian and Himalayan spiritual communities often constructed temples and fortifications on design plans of mandala and yantra. For examples of sacred geometry in art and architecture refer:
Labyrinth (an Eulerian path, as distinct from a maze) Mandala – Parthenon -Taijitu (Yin-Yang) - Tree of Life - Rose Window Celtic art such as the Book of Kells – Yantra - Dharmacakra
The golden ratio, also known as the gold ratio, golden proportion, golden mean, golden section, golden number, divine proportion or sectio divina, is an irrational number, approximately 1.618 033 988 749 894 848, that possesses many interesting properties.
Shapes proportioned according to the golden ratio have long been considered aesthetically pleasing in Western cultures, and the golden ratio is still used frequently in art and design, suggesting a natural balance between symmetry and asymmetry.
The ancient Pythagoreans, who defined numbers as expressions of ratios (and not as units as is common today), believed that reality is numerical and that the golden ratio expressed an underlying truth about existence.
Since the Renaissance, many artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing.
Mathematicians have studied the golden ratio because of its unique and interesting properties.
🌸
🌸
Fibonacci Numbers
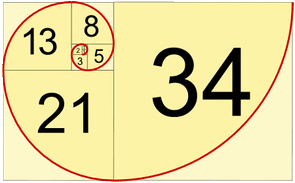
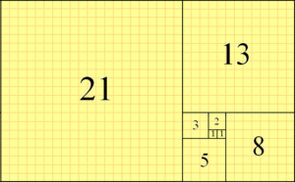
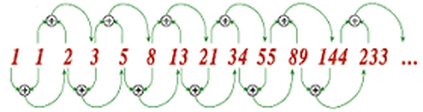
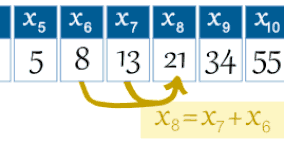
By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Some sources omit the initial 0, instead beginning the sequence with two 1s.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation with seed values.
The Fibonacci sequence is named after Leonardo of Pisa, who was known as Fibonacci (a contraction of filius Bonacci, "son of Bonaccio"). Fibonacci's 1202 book Liber Abaci introduced the sequence to Western European mathematics, although the sequence may have been previously described in Indian mathematics.
Fibonacci numbers are used in the analysis of financial markets, in strategies such as Fibonacci retracement, and are used in computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure.
The simple recursion of Fibonacci numbers has also inspired a family of
recursive graphs called Fibonacci cubes for interconnecting parallel and distributed systems.
They also appear in biological settings, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.
🌸
Fibonacci Numbers
By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Some sources omit the initial 0, instead beginning the sequence with two 1s.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation with seed values.
The Fibonacci sequence is named after Leonardo of Pisa, who was known as Fibonacci (a contraction of filius Bonacci, "son of Bonaccio"). Fibonacci's 1202 book Liber Abaci introduced the sequence to Western European mathematics, although the sequence may have been previously described in Indian mathematics.
Fibonacci numbers are used in the analysis of financial markets, in strategies such as Fibonacci retracement, and are used in computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure.
The simple recursion of Fibonacci numbers has also inspired a family of
recursive graphs called Fibonacci cubes for interconnecting parallel and distributed systems.
They also appear in biological settings, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.
🌸
🌸
Leonardo Fibonacci
Biography
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Fibonacci#cite_note-Knott-2
Fibonacci number.
Liber Abaci, popularizing the Hindu–Arabic numeral system in Europe
Fibonacci numbers
Parent(s) Guglielmo Bonacci Leonardo Bonacci (c. 1170 – c. 1250) [2]—known as Fibonacci (Italian: [fiboˈnattʃi]), and Leonardo of Pisa, Leonardo Pisano Bigollo, Leonardo Fibonacci
was an Italian mathematician,
considered to be "the most talented Western mathematician of the Middle Ages". [3][4]
Fibonacci popularized the Hindu–Arabic numeral system to the Western World [5] primarily through his composition in 1202 of Liber Abaci (Book of Calculation). [6]
He also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in Liber Abaci. [7]
Leonardo Fibonacci
Biography
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Fibonacci#cite_note-Knott-2
Fibonacci number.
Liber Abaci, popularizing the Hindu–Arabic numeral system in Europe
Fibonacci numbers
Parent(s) Guglielmo Bonacci Leonardo Bonacci (c. 1170 – c. 1250) [2]—known as Fibonacci (Italian: [fiboˈnattʃi]), and Leonardo of Pisa, Leonardo Pisano Bigollo, Leonardo Fibonacci
was an Italian mathematician,
considered to be "the most talented Western mathematician of the Middle Ages". [3][4]
Fibonacci popularized the Hindu–Arabic numeral system to the Western World [5] primarily through his composition in 1202 of Liber Abaci (Book of Calculation). [6]
He also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in Liber Abaci. [7]
🌸
Fibonacci was born around 1170 to Guglielmo Bonacci, a wealthy Italian merchant and, by some accounts, the consul for Pisa. Guglielmo directed a trading post in Bugia, a port in the Almohad dynasty's sultanate in North Africa. Fibonacci travelled with him as a young boy, and it was in Bugia (now Béjaïa, Algeria) that he learned about the Hindu–Arabic numeral system. [2]
Fibonacci travelled extensively around the Mediterranean coast, meeting with many merchants and learning about their systems of doing arithmetic. He soon realised the many advantages of the Hindu-Arabic system. In 1202, he completed the Liber Abaci (Book of Abacus or Book of Calculation) which popularized Hindu–Arabic numerals in Europe. [2]
Fibonacci became a guest of Emperor Frederick II, who enjoyed mathematics and science. In 1240, the Republic of Pisa honored Fibonacci (referred to as Leonardo Bigollo)[8] by granting him a salary in a decree that recognized him for the services that he had given to the city as an advisor on matters of accounting and instruction to citizens. [9]
The date of Fibonacci's death is not known, but it has been estimated to be between 1240 [10] and 1250, [11] most likely in Pisa.
Fibonacci was born around 1170 to Guglielmo Bonacci, a wealthy Italian merchant and, by some accounts, the consul for Pisa. Guglielmo directed a trading post in Bugia, a port in the Almohad dynasty's sultanate in North Africa. Fibonacci travelled with him as a young boy, and it was in Bugia (now Béjaïa, Algeria) that he learned about the Hindu–Arabic numeral system. [2]
Fibonacci travelled extensively around the Mediterranean coast, meeting with many merchants and learning about their systems of doing arithmetic. He soon realised the many advantages of the Hindu-Arabic system. In 1202, he completed the Liber Abaci (Book of Abacus or Book of Calculation) which popularized Hindu–Arabic numerals in Europe. [2]
Fibonacci became a guest of Emperor Frederick II, who enjoyed mathematics and science. In 1240, the Republic of Pisa honored Fibonacci (referred to as Leonardo Bigollo)[8] by granting him a salary in a decree that recognized him for the services that he had given to the city as an advisor on matters of accounting and instruction to citizens. [9]
The date of Fibonacci's death is not known, but it has been estimated to be between 1240 [10] and 1250, [11] most likely in Pisa.
🌸
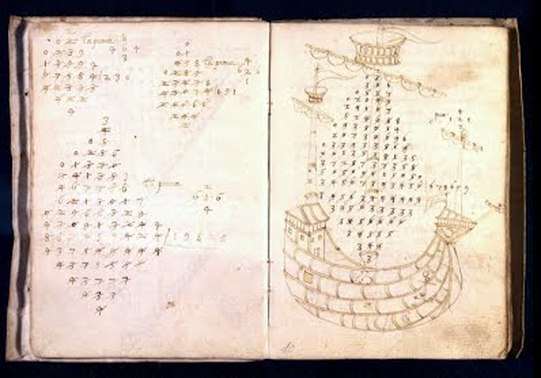
Liber Abaci (1202)
Pages of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze showing the Fibonacci sequence with the position in the sequence labeled in Roman numerals and the value in Hindu-Arabic numerals.
🌸
Liber Abaci (1202)
Pages of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze showing the Fibonacci sequence with the position in the sequence labeled in Roman numerals and the value in Hindu-Arabic numerals.
🌸
🌸
The Man of Numbers
In Search of Leonardo Fibonacci
A Free PDF to Download
https://www.maa.org/external_archive/devlin/Fibonacci.pdf
🌸
The Man of Numbers
In Search of Leonardo Fibonacci
A Free PDF to Download
https://www.maa.org/external_archive/devlin/Fibonacci.pdf
🌸
🌸
In the Liber Abaci
(1202)...
Liber Abaci
In the Liber Abaci (1202), Fibonacci introduced the so-called modus Indorum (method of the Indians), today known as Hindu-Arabic numerals. [12][13] The book advocated numeration with the digits 0–9 and place value. The book showed the practical use and value of the new Arabic numeral system by applying the numerals to commercial bookkeeping, converting weights and measures, calculation of interest, money-changing, and other applications.
The book was well-received throughout educated Europe and had a profound impact on European thought. No copies of the 1202 edition are known to exist. [14]
The 1228 edition, first section introduces the Arabic numeral system and compares the system with other systems, such as Roman numerals, and methods to convert the other numeral systems into Arabic numerals. Replacing the Roman numeral system, its ancient Egyptian multiplication method, and using an abacus for calculations, with an Arabic numeral system was an advance in making business calculations easier and faster, which led to the growth of banking and accounting in Europe. [15][16]
The second section explains the uses of Arabic numerals in business, for example converting different currencies, and calculating profit and interest, which were important to the growing banking industry. The book also discusses irrational numbers and prime numbers. [14][15][16]
Fibonacci sequence.
Main article: Fibonacci number
Liber Abaci posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers.
Although Fibonacci's Liber Abaci contains the earliest known description of the sequence outside of India, the sequence had been noted by Indian mathematicians as early as the sixth century. [17][18][19][20]
In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers.
Fibonacci began the sequence not with 0, 1, 1, 2, as modern mathematicians do but with 1,1, 2, etc. He carried the calculation up to the thirteenth place (fourteenth in modern counting), that is 233, though another manuscript carries it to the next place:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. [21][22]
Fibonacci did not speak about the golden ratio as the limit of the ratio of
consecutive numbers in this sequence.
Legacy
In the 19th century, a statue of Fibonacci was constructed and raised in Pisa. Today it is located in the western gallery of the Camposanto, historical cemetery on the Piazza dei Miracoli. [23]
There are many mathematical concepts named after Fibonacci because of a connection to the Fibonacci numbers. Examples include the Brahmagupta–Fibonacci identity, the Fibonacci search technique, and the Pisano period. Beyond mathematics, namesakes of Fibonacci include the asteroid 6765 Fibonacci and the art rock band The Fibonaccis.
In the Liber Abaci
(1202)...
Liber Abaci
In the Liber Abaci (1202), Fibonacci introduced the so-called modus Indorum (method of the Indians), today known as Hindu-Arabic numerals. [12][13] The book advocated numeration with the digits 0–9 and place value. The book showed the practical use and value of the new Arabic numeral system by applying the numerals to commercial bookkeeping, converting weights and measures, calculation of interest, money-changing, and other applications.
The book was well-received throughout educated Europe and had a profound impact on European thought. No copies of the 1202 edition are known to exist. [14]
The 1228 edition, first section introduces the Arabic numeral system and compares the system with other systems, such as Roman numerals, and methods to convert the other numeral systems into Arabic numerals. Replacing the Roman numeral system, its ancient Egyptian multiplication method, and using an abacus for calculations, with an Arabic numeral system was an advance in making business calculations easier and faster, which led to the growth of banking and accounting in Europe. [15][16]
The second section explains the uses of Arabic numerals in business, for example converting different currencies, and calculating profit and interest, which were important to the growing banking industry. The book also discusses irrational numbers and prime numbers. [14][15][16]
Fibonacci sequence.
Main article: Fibonacci number
Liber Abaci posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers.
Although Fibonacci's Liber Abaci contains the earliest known description of the sequence outside of India, the sequence had been noted by Indian mathematicians as early as the sixth century. [17][18][19][20]
In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers.
Fibonacci began the sequence not with 0, 1, 1, 2, as modern mathematicians do but with 1,1, 2, etc. He carried the calculation up to the thirteenth place (fourteenth in modern counting), that is 233, though another manuscript carries it to the next place:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. [21][22]
Fibonacci did not speak about the golden ratio as the limit of the ratio of
consecutive numbers in this sequence.
Legacy
In the 19th century, a statue of Fibonacci was constructed and raised in Pisa. Today it is located in the western gallery of the Camposanto, historical cemetery on the Piazza dei Miracoli. [23]
There are many mathematical concepts named after Fibonacci because of a connection to the Fibonacci numbers. Examples include the Brahmagupta–Fibonacci identity, the Fibonacci search technique, and the Pisano period. Beyond mathematics, namesakes of Fibonacci include the asteroid 6765 Fibonacci and the art rock band The Fibonaccis.
| Albrecht Durer | |
| File Size: | 2711 kb |
| File Type: | pps |
🌸
Albrecht Dürer
was a German painter, printmaker, and theorist of the German Renaissance.
Born in Hungary, Dürer established his reputation and influence across Europe
in his twenties due to his high-quality woodcut prints.
Wikipedia
🌸
His ancestors came from Ajtós (Eytas) near Gyula,
the name of the village was used as a noble prefix ("ajtósi" in German Türer).
Albrecht Dürer arrived in Nuremberg on 11 March 1455, aged 28.
🌸
Born: May 21, 1471, Hungary
Died: April 6, 1528, Nuremberg, Germany
Spouse: Agnes Dürer (m. 1494–1528)
Periods: Northern Renaissance, German Renaissance, Gothic art
Parents: Barbara Dürer, Albrecht Dürer the Elder
Siblings: Hans Dürer
🌸
Albrecht Dürer
was a German painter, printmaker, and theorist of the German Renaissance.
Born in Hungary, Dürer established his reputation and influence across Europe
in his twenties due to his high-quality woodcut prints.
Wikipedia
🌸
His ancestors came from Ajtós (Eytas) near Gyula,
the name of the village was used as a noble prefix ("ajtósi" in German Türer).
Albrecht Dürer arrived in Nuremberg on 11 March 1455, aged 28.
🌸
Born: May 21, 1471, Hungary
Died: April 6, 1528, Nuremberg, Germany
Spouse: Agnes Dürer (m. 1494–1528)
Periods: Northern Renaissance, German Renaissance, Gothic art
Parents: Barbara Dürer, Albrecht Dürer the Elder
Siblings: Hans Dürer
🌸
🌸
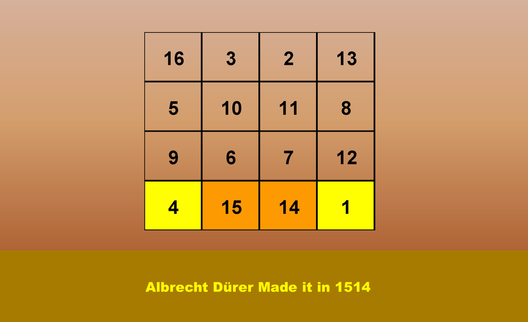
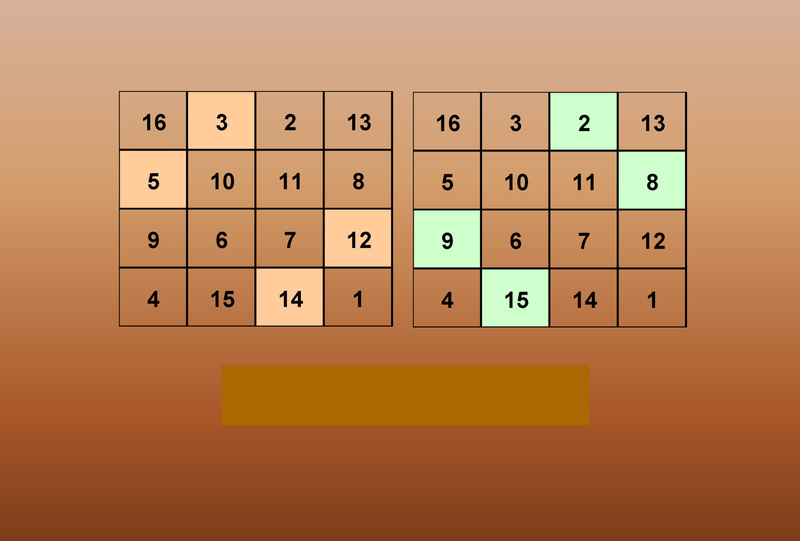
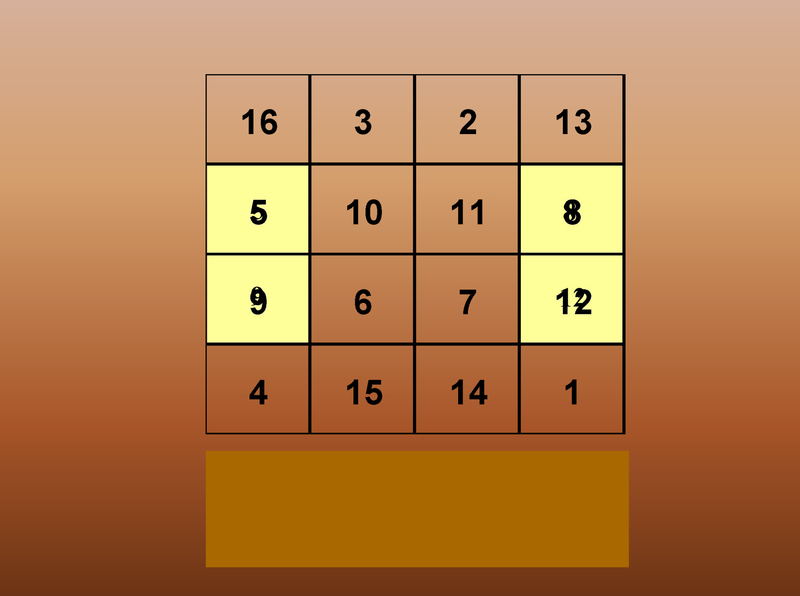
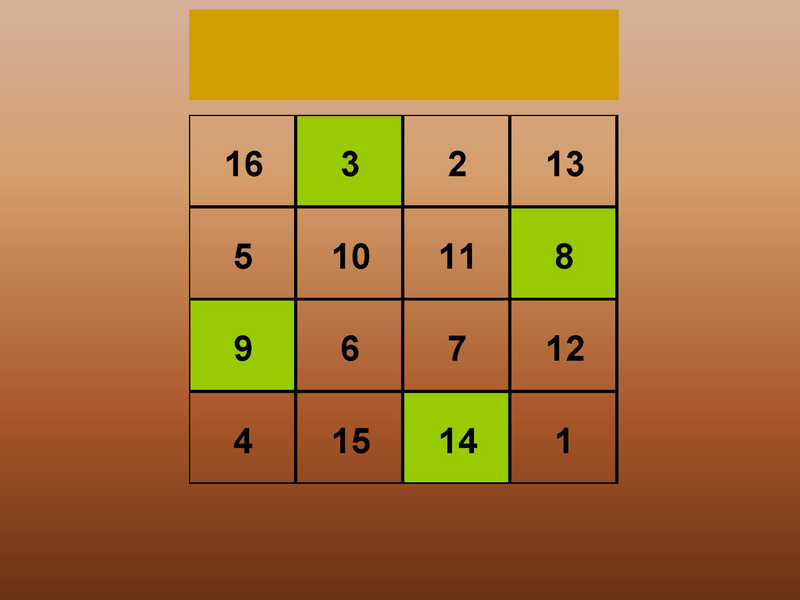
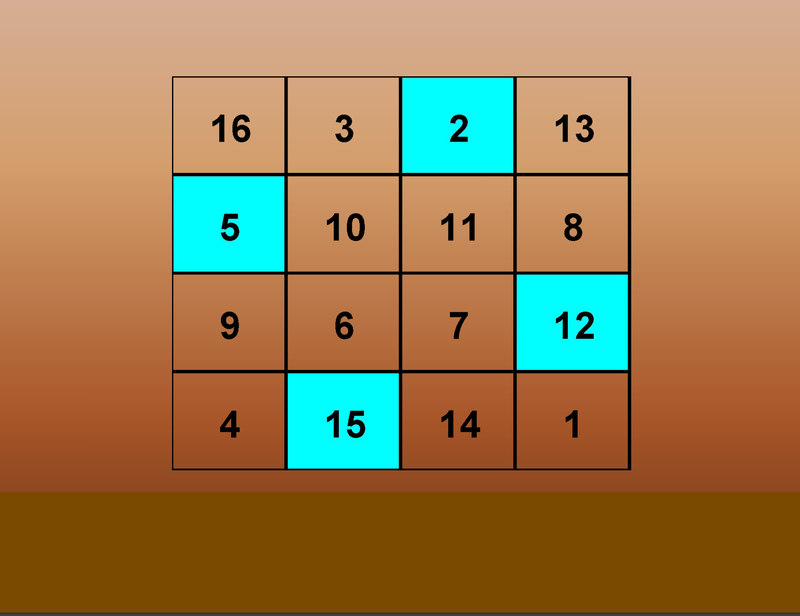
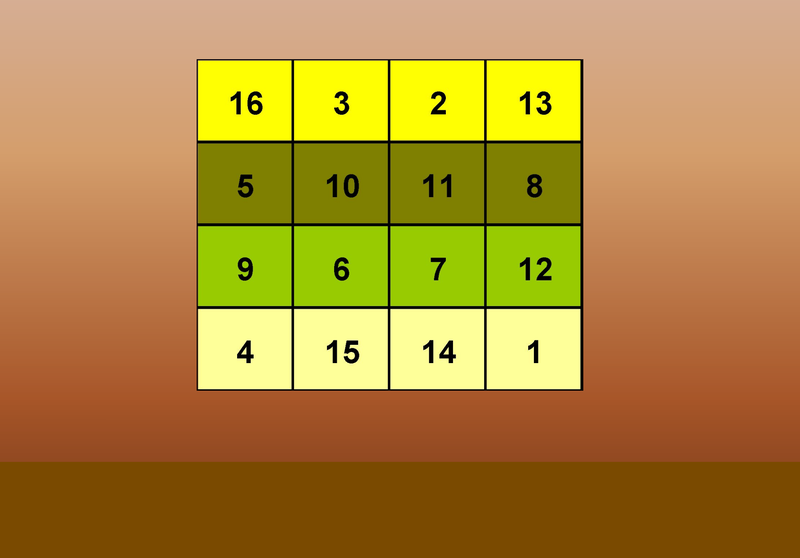
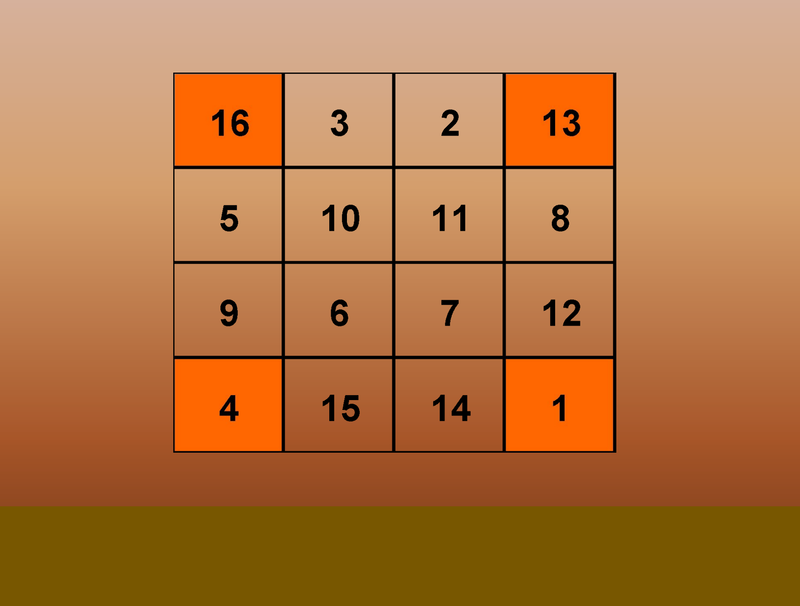
All the Numbers Added Up to
34
🌸
All the Numbers Added Up to
34
🌸
🌸
Le Corbusier / The Swiss Architect
His Book: Der Modulor
Charles-Édouard Jeanneret-Gris, who was better known as Le Corbusier,
was a Swiss - French architect, designer, painter, urban planner,
writer, and one of the pioneers of modern architecture. Wikipedia
Born: October 6, 1887, La Chaux-de-Fonds, Switzerland
Died: August 27, 1965, Roquebrune-Cap-Martin, France
Le Corbusier 's faith in the mathematical order of the universe was closely bound to
the golden ratio and the Fibonacci series, which he described as "rhythms apparent to the eye and clear in their relations with one another.
Modulor: Le Corbusier explicitly used the golden ratio in his system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci's "Vitruvian Man", the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture.
In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took Leonardo's suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body's height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system.[47]
His Book: Der Modulor
Charles-Édouard Jeanneret-Gris, who was better known as Le Corbusier,
was a Swiss - French architect, designer, painter, urban planner,
writer, and one of the pioneers of modern architecture. Wikipedia
Born: October 6, 1887, La Chaux-de-Fonds, Switzerland
Died: August 27, 1965, Roquebrune-Cap-Martin, France
Le Corbusier 's faith in the mathematical order of the universe was closely bound to
the golden ratio and the Fibonacci series, which he described as "rhythms apparent to the eye and clear in their relations with one another.
Modulor: Le Corbusier explicitly used the golden ratio in his system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci's "Vitruvian Man", the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture.
In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took Leonardo's suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body's height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system.[47]
Buildings by Le Corbusier:
The United Nations Headquarters, New York. 1947
Chapel of Notre Dame du Haut, Ronchamp, Belfort, France. 1954
The United Nations Headquarters, New York. 1947
Chapel of Notre Dame du Haut, Ronchamp, Belfort, France. 1954
The Open Hand (La Main Ouverte) is a Le Corbusier's architecture,
a sign for him of.
a sign for him of.
"Peace and reconciliation,
it is open to give and open to receive."
The largest sculptures that Le Corbusier created is a 26 meter high version.
Known as the Open Hand Monument.
Located: Chandigarh, India / 30.758974°N 76.807348°E
Artist: Le Corbusier / Year 1964
Dimensions: 26 m (85 ft)
it is open to give and open to receive."
The largest sculptures that Le Corbusier created is a 26 meter high version.
Known as the Open Hand Monument.
Located: Chandigarh, India / 30.758974°N 76.807348°E
Artist: Le Corbusier / Year 1964
Dimensions: 26 m (85 ft)
Back side of the Swiss 10 CHF banknote, showing the Modulor
0, 1 + 1 = 2 / 1 + 2 = 3 / 2 + 3 = 5 / 3 + 5 = 8. Etc. 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …