🌸
Fibonacci Harmóniák
https://www.eletesegeszseg.com/fibonocci-harmoniaacutek.html
🌸
Fibonacci-számok
A Fibonacci-számok
a matematikában az egyik legismertebb másodrendben rekurzív sorozat elemei.
🌸
Fibonacci Harmóniák
https://www.eletesegeszseg.com/fibonocci-harmoniaacutek.html
🌸
Fibonacci-számok
A Fibonacci-számok
a matematikában az egyik legismertebb másodrendben rekurzív sorozat elemei.
🌸
🌸
Mit Jelentenek a Fibonacci - Számok?
🌸
Mit Jelentenek a Fibonacci - Számok?
🌸
| Mit Jelentenek a Fibonacci - Számok? | |
| File Size: | 2043 kb |
| File Type: | |
🌸
🌸
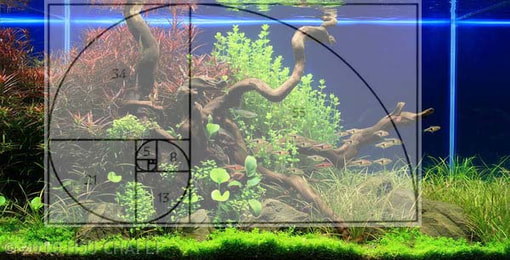
Ha megnézzük a napraforgót, spirális alakot látunk.
Ez pontosan 21 vagy 34, attól függően, hogy melyik irányba nézzük.
🌸
Ha megnézzük a napraforgót, spirális alakot látunk.
Ez pontosan 21 vagy 34, attól függően, hogy melyik irányba nézzük.
🌸
🌸
Az Aranyszám
Körülbelül
1.618 033 988 749 894 848
🌸
Az Aranyszám
Körülbelül
1.618 033 988 749 894 848
🌸
🌸
1150-ben fedezték fel ...
és két indiai matematikus írta le Gopala és Hemacsandra,
akik a szanszkrit prozódia elméleti aspektusait vizsgálták.
Susantha Goonatilake azt írja, hogy a Fibonacci-sorozat kialakulása
"részben Pingalának (i. e. 200) tulajdonítják, később Virahankával (i. sz. 700 körül) hozták kapcsolatba, Gopāla (1135 körül) és Hemachandra (1150 körül)"
A sorrend legvilágosabb kifejtése azonban Virahanka (Kr. u. 700 körül) művében merül fel,
akinek saját műve elveszett, de Gopāla (1135 körül) egy idézetében elérhető:
A szekvenciát Gopala (Kr. u. 1135 előtt) és a dzsainok is tárgyalják. Hemachandra (1150 körül).
és két indiai matematikus írta le Gopala és Hemacsandra,
akik a szanszkrit prozódia elméleti aspektusait vizsgálták.
Susantha Goonatilake azt írja, hogy a Fibonacci-sorozat kialakulása
"részben Pingalának (i. e. 200) tulajdonítják, később Virahankával (i. sz. 700 körül) hozták kapcsolatba, Gopāla (1135 körül) és Hemachandra (1150 körül)"
A sorrend legvilágosabb kifejtése azonban Virahanka (Kr. u. 700 körül) művében merül fel,
akinek saját műve elveszett, de Gopāla (1135 körül) egy idézetében elérhető:
A szekvenciát Gopala (Kr. u. 1135 előtt) és a dzsainok is tárgyalják. Hemachandra (1150 körül).
🌸
Fibonacci - Számok
Az aranymetszést, a geometriai arányokat és a geometriai számokat gyakran alkalmazták az egyiptomi, ókori indiai, görög és római építészet tervezésénél.
A középkori európai katedrálisok is beépítettek szimbolikus geometriát.
Az indiai és himalájai spirituális közösségek gyakran építettek templomokat és erődítményeket mandala és yantra tervrajzok alapján.
A szakrális geometria példáit a művészetben és az építészetben lásd:
Labirintus (Euler-ösvény, megkülönböztetve a labirintustól) Mandala - Parthenon -Taijitu (Yin-Yang) - Életfa - Rózsaablak Kelta művészet, mint például a Kells könyve - Yantra - Dharmacakra.
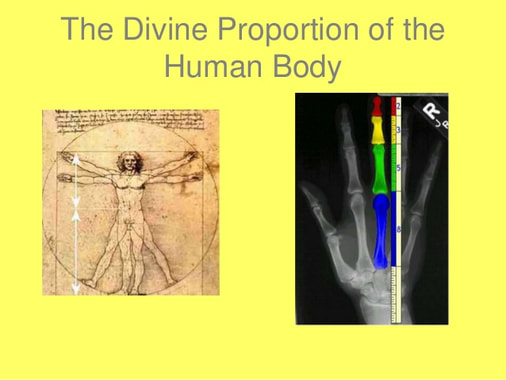
Az aranymetszés, más néven arany arány, arany középút, aranyszám, isteni arány vagy sectio divina, egy irracionális szám,
körülbelül 1,618 033 988 749 894 848,
amely számos érdekes tulajdonsággal rendelkezik.
Az aranymetszés szerint arányos alakzatokat a nyugati kultúrákban régóta esztétikusnak tartják,
és az aranymetszést a művészetben és a formatervezésben még ma is gyakran használják,
a szimmetria és az aszimmetria természetes egyensúlyát sugallva.
Az ókori püthagoreusok, akik a számokat arányok kifejezéseként határozták meg (és nem egységként, ahogyan az manapság szokásos), úgy vélték, hogy a valóság számszerű,
és hogy az aranymetszés a létezés egy mögöttes igazságát fejezi ki.
A reneszánsz óta sok művész és építész úgy arányosította műveit, hogy azok megközelítsék
az aranymetszést - különösen az aranytéglalap formájában,
amelyben a hosszabbik oldal és a rövidebbik oldal aránya az aranymetszés -,
mivel úgy vélték, hogy ez az arány esztétikailag kellemes.
A matematikusok az aranymetszést egyedi és érdekes tulajdonságai miatt tanulmányozták.
🌸
Fibonacci - Számok
Az aranymetszést, a geometriai arányokat és a geometriai számokat gyakran alkalmazták az egyiptomi, ókori indiai, görög és római építészet tervezésénél.
A középkori európai katedrálisok is beépítettek szimbolikus geometriát.
Az indiai és himalájai spirituális közösségek gyakran építettek templomokat és erődítményeket mandala és yantra tervrajzok alapján.
A szakrális geometria példáit a művészetben és az építészetben lásd:
Labirintus (Euler-ösvény, megkülönböztetve a labirintustól) Mandala - Parthenon -Taijitu (Yin-Yang) - Életfa - Rózsaablak Kelta művészet, mint például a Kells könyve - Yantra - Dharmacakra.
Az aranymetszés, más néven arany arány, arany középút, aranyszám, isteni arány vagy sectio divina, egy irracionális szám,
körülbelül 1,618 033 988 749 894 848,
amely számos érdekes tulajdonsággal rendelkezik.
Az aranymetszés szerint arányos alakzatokat a nyugati kultúrákban régóta esztétikusnak tartják,
és az aranymetszést a művészetben és a formatervezésben még ma is gyakran használják,
a szimmetria és az aszimmetria természetes egyensúlyát sugallva.
Az ókori püthagoreusok, akik a számokat arányok kifejezéseként határozták meg (és nem egységként, ahogyan az manapság szokásos), úgy vélték, hogy a valóság számszerű,
és hogy az aranymetszés a létezés egy mögöttes igazságát fejezi ki.
A reneszánsz óta sok művész és építész úgy arányosította műveit, hogy azok megközelítsék
az aranymetszést - különösen az aranytéglalap formájában,
amelyben a hosszabbik oldal és a rövidebbik oldal aránya az aranymetszés -,
mivel úgy vélték, hogy ez az arány esztétikailag kellemes.
A matematikusok az aranymetszést egyedi és érdekes tulajdonságai miatt tanulmányozták.
🌸
🌸
Fibonacci - Számok
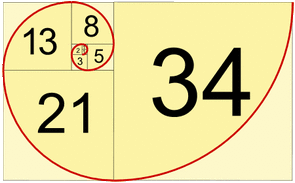
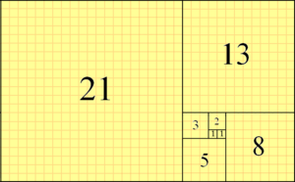
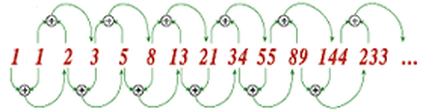
Definíció szerint az első két Fibonacci-szám 0 és 1,
és minden további szám az előző kettő összege.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Egyes források kihagyják a kezdeti 0-t, és helyette két 1-essel kezdik a sorozatot.
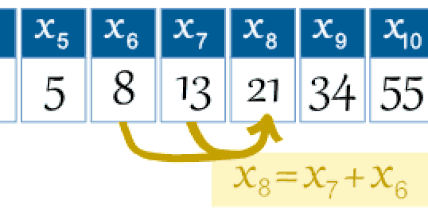
Matematikai értelemben a Fibonacci-számok Fn sorozatát
a rekurzív összefüggés határozza meg a kezdőértékekkel.
A Fibonacci-sorozatot a pisai Leonardo után nevezték el, akit Fibonacci néven ismertek (a filius Bonacci, "Bonaccio fia" rövidítése).
Fibonacci 1202-ben megjelent Liber Abaci című könyve vezette be a sorozatot a nyugat-európai matematikába, bár a sorozatot már korábban is leírhatták az indiai matematikában.
A Fibonacci-számokat használják a pénzügyi piacok elemzésében, az olyan stratégiákban, mint a Fibonacci retracement, és olyan számítógépes algoritmusokban, mint a Fibonacci-keresési technika és a Fibonacci-halom adatszerkezet.
A Fibonacci-számok egyszerű rekurziója inspirálta a Fibonacci-számok egy családját is.
rekurzív gráfokat, a Fibonacci-kockákat, a párhuzamos és elosztott rendszerek összekapcsolására.
Ezek a számok biológiai környezetben is megjelennek, mint például a fák elágazása,
a levelek elrendeződése a száron, az ananász gyümölcsei, az articsóka virágzása,
a páfrányok kibomlása és a fenyőtobozok elrendeződése.
Fibonacci - Számok
Definíció szerint az első két Fibonacci-szám 0 és 1,
és minden további szám az előző kettő összege.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Egyes források kihagyják a kezdeti 0-t, és helyette két 1-essel kezdik a sorozatot.
Matematikai értelemben a Fibonacci-számok Fn sorozatát
a rekurzív összefüggés határozza meg a kezdőértékekkel.
A Fibonacci-sorozatot a pisai Leonardo után nevezték el, akit Fibonacci néven ismertek (a filius Bonacci, "Bonaccio fia" rövidítése).
Fibonacci 1202-ben megjelent Liber Abaci című könyve vezette be a sorozatot a nyugat-európai matematikába, bár a sorozatot már korábban is leírhatták az indiai matematikában.
A Fibonacci-számokat használják a pénzügyi piacok elemzésében, az olyan stratégiákban, mint a Fibonacci retracement, és olyan számítógépes algoritmusokban, mint a Fibonacci-keresési technika és a Fibonacci-halom adatszerkezet.
A Fibonacci-számok egyszerű rekurziója inspirálta a Fibonacci-számok egy családját is.
rekurzív gráfokat, a Fibonacci-kockákat, a párhuzamos és elosztott rendszerek összekapcsolására.
Ezek a számok biológiai környezetben is megjelennek, mint például a fák elágazása,
a levelek elrendeződése a száron, az ananász gyümölcsei, az articsóka virágzása,
a páfrányok kibomlása és a fenyőtobozok elrendeződése.
🌸
🌸
Leonardo Fibonacci
Életrajza
Született. 1170 - 75
Elhunyt 1240 - 50 / Valószínűleg Pisa
https://hu.wikipedia.org/wiki/Fibonacci
Leonardo Fibonacci
Életrajza
Született. 1170 - 75
Elhunyt 1240 - 50 / Valószínűleg Pisa
https://hu.wikipedia.org/wiki/Fibonacci
🌸
Szülő(k) Guglielmo Bonacci Leonardo Bonacci (1170 körül - 1250 körül) -
ismert Fibonacci, illetve Leonardo of Pisa, Leonardo Pisano Bigollo, Leonardo Fibonacci.
olasz matematikus volt, akit "a középkor legtehetségesebb nyugati matematikusának" tartottak.
Fibonacci népszerűsítette a hindu-arab számrendszert a nyugati világban elsősorban a Liber Abaci (Számolás könyve) című 1202-ben megjelent művével.
Ő ismertette meg Európát a Fibonacci-számok sorozatával is,
amelyet példaként használt a Liber Abaciban.
🌸
Szülő(k) Guglielmo Bonacci Leonardo Bonacci (1170 körül - 1250 körül) -
ismert Fibonacci, illetve Leonardo of Pisa, Leonardo Pisano Bigollo, Leonardo Fibonacci.
olasz matematikus volt, akit "a középkor legtehetségesebb nyugati matematikusának" tartottak.
Fibonacci népszerűsítette a hindu-arab számrendszert a nyugati világban elsősorban a Liber Abaci (Számolás könyve) című 1202-ben megjelent művével.
Ő ismertette meg Európát a Fibonacci-számok sorozatával is,
amelyet példaként használt a Liber Abaciban.
🌸
Fibonacci 1170 körül született Guglielmo Bonacci, egy gazdag olasz kereskedő és egyes beszámolók szerint pisai konzul gyermekeként.
Guglielmo egy kereskedelmi állomást vezetett Bugiában, az Almohád dinasztia észak-afrikai szultánságának egyik kikötőjében. Fibonacci fiatal fiúként vele utazott, és Bugiában (ma Béjaïa, Algéria) ismerkedett meg a hindu-arab számrendszerrel.
Fibonacci sokat utazott a Földközi-tenger partvidékén, számos kereskedővel találkozott, és megismerte számtani rendszereiket.
Hamarosan rájött a hindu-arab számrendszer számos előnyére. 1202-ben elkészítette a Liber Abaci (Abakusz- vagy Számítási könyv) című művét, amely népszerűsítette a hindu-arab számrendszer használatát Európában.
Fibonacci a matematikát és a tudományokat kedvelő II. frigyes császár vendége lett.
1240-ben a pisai köztársaság azzal tisztelgett Fibonacci (akit Leonardo Bigollo néven emlegettek) előtt, hogy egy rendeletben fizetést adományozott neki, amelyben elismerte a városnak nyújtott szolgálatait, amelyeket számviteli kérdésekben és a polgárok oktatásában tanácsadóként nyújtott.
Fibonacci halálának időpontja nem ismert, de a becslések szerint 1240
és 1250 között lehetett, valószínűleg Pisában.
🌸
Guglielmo egy kereskedelmi állomást vezetett Bugiában, az Almohád dinasztia észak-afrikai szultánságának egyik kikötőjében. Fibonacci fiatal fiúként vele utazott, és Bugiában (ma Béjaïa, Algéria) ismerkedett meg a hindu-arab számrendszerrel.
Fibonacci sokat utazott a Földközi-tenger partvidékén, számos kereskedővel találkozott, és megismerte számtani rendszereiket.
Hamarosan rájött a hindu-arab számrendszer számos előnyére. 1202-ben elkészítette a Liber Abaci (Abakusz- vagy Számítási könyv) című művét, amely népszerűsítette a hindu-arab számrendszer használatát Európában.
Fibonacci a matematikát és a tudományokat kedvelő II. frigyes császár vendége lett.
1240-ben a pisai köztársaság azzal tisztelgett Fibonacci (akit Leonardo Bigollo néven emlegettek) előtt, hogy egy rendeletben fizetést adományozott neki, amelyben elismerte a városnak nyújtott szolgálatait, amelyeket számviteli kérdésekben és a polgárok oktatásában tanácsadóként nyújtott.
Fibonacci halálának időpontja nem ismert, de a becslések szerint 1240
és 1250 között lehetett, valószínűleg Pisában.
🌸
🌸
Fibonacci (1202) - ben
bevezette az úgynevezett modus Indorumot (az indiaiak módszere), amelyet ma hindu-arab számjegyekként ismerünk. A könyv a 0-9 számjegyekkel és helyértékkel történő számolást támogatta.
A könyv az új arab számrendszer gyakorlati alkalmazását és értékét mutatta be a számjegyek kereskedelmi könyvelésben, a súlyok és mértékek átváltásában, a kamatszámításban,
a pénzváltásban és más alkalmazásokban való alkalmazásával.
A könyv az egész művelt Európában nagy visszhangot váltott ki,
és nagy hatással volt az európai gondolkodásra.
Az 1202-es kiadásból nem ismert egyetlen példány sem.
Az 1228-as kiadás első része bemutatja az arab számrendszert, és összehasonlítja a rendszert más rendszerekkel, például a római számokkal, valamint a más számrendszerek arab számokká való átalakításának módszereit.
A római számrendszer, annak ókori egyiptomi szorzási módszere és az abakusz használata a számításokhoz az arab számrendszerrel való felváltása előrelépés volt az üzleti számítások egyszerűbbé és gyorsabbá tételében, ami a banki és számviteli tevékenység fejlődéséhez vezetett Európában.
A második fejezet az arab számok üzleti felhasználását ismerteti, például a különböző pénznemek átváltását, valamint a nyereség és a kamatok kiszámítását, amelyek fontosak voltak a növekvő bankszektor számára. A könyv tárgyalja az irracionális számokat és a prímszámokat is.
Fibonacci-sorozat.
🌸
Liber Abaci egy nyúlpopuláció növekedésével kapcsolatos problémát tett fel
és oldott meg idealizált feltételezések alapján.
A megoldás, generációról generációra, egy számsorozat volt, amelyet később Fibonacci-számokként ismertek.
Bár Fibonacci Liber Abaci című műve tartalmazza a sorozat legkorábbi ismert, Indián kívüli leírását, a sorozatot már a hatodik században feljegyezték indiai matematikusok.
A Fibonacci-számsorozatban minden szám az előző két szám összege.
Fibonacci a sorozatot nem 0, 1, 1, 1, 2-vel kezdte, mint a modern matematikusok,
hanem 1,1, 2 stb. kezdetűvel.
A számítást a tizenharmadik (modern számolásban tizennegyedik) helyig, azaz a 233-ig vitte,
bár egy másik kézirat a következő helyig viszi:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Fibonacci nem beszélt az aranymetszésről, mint az arányok határértékéről.
Az egymás utáni számok aránya ebben a sorozatban.
🌸
A 19. században Pisában Fibonacci szobrot állítottak és emeltek. Ma a Camposanto nyugati galériáján, a Piazza dei Miracoli történelmi temetőben található.
Számos matematikai fogalmat neveztek el Fibonacciról, mert a Fibonacci-számokhoz kapcsolódik. Ilyen például a Brahmagupta-Fibonacci azonosság,
a Fibonacci-keresési technika és a Pisano periódus.
Fibonacci (1202) - ben
bevezette az úgynevezett modus Indorumot (az indiaiak módszere), amelyet ma hindu-arab számjegyekként ismerünk. A könyv a 0-9 számjegyekkel és helyértékkel történő számolást támogatta.
A könyv az új arab számrendszer gyakorlati alkalmazását és értékét mutatta be a számjegyek kereskedelmi könyvelésben, a súlyok és mértékek átváltásában, a kamatszámításban,
a pénzváltásban és más alkalmazásokban való alkalmazásával.
A könyv az egész művelt Európában nagy visszhangot váltott ki,
és nagy hatással volt az európai gondolkodásra.
Az 1202-es kiadásból nem ismert egyetlen példány sem.
Az 1228-as kiadás első része bemutatja az arab számrendszert, és összehasonlítja a rendszert más rendszerekkel, például a római számokkal, valamint a más számrendszerek arab számokká való átalakításának módszereit.
A római számrendszer, annak ókori egyiptomi szorzási módszere és az abakusz használata a számításokhoz az arab számrendszerrel való felváltása előrelépés volt az üzleti számítások egyszerűbbé és gyorsabbá tételében, ami a banki és számviteli tevékenység fejlődéséhez vezetett Európában.
A második fejezet az arab számok üzleti felhasználását ismerteti, például a különböző pénznemek átváltását, valamint a nyereség és a kamatok kiszámítását, amelyek fontosak voltak a növekvő bankszektor számára. A könyv tárgyalja az irracionális számokat és a prímszámokat is.
Fibonacci-sorozat.
🌸
Liber Abaci egy nyúlpopuláció növekedésével kapcsolatos problémát tett fel
és oldott meg idealizált feltételezések alapján.
A megoldás, generációról generációra, egy számsorozat volt, amelyet később Fibonacci-számokként ismertek.
Bár Fibonacci Liber Abaci című műve tartalmazza a sorozat legkorábbi ismert, Indián kívüli leírását, a sorozatot már a hatodik században feljegyezték indiai matematikusok.
A Fibonacci-számsorozatban minden szám az előző két szám összege.
Fibonacci a sorozatot nem 0, 1, 1, 1, 2-vel kezdte, mint a modern matematikusok,
hanem 1,1, 2 stb. kezdetűvel.
A számítást a tizenharmadik (modern számolásban tizennegyedik) helyig, azaz a 233-ig vitte,
bár egy másik kézirat a következő helyig viszi:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
Fibonacci nem beszélt az aranymetszésről, mint az arányok határértékéről.
Az egymás utáni számok aránya ebben a sorozatban.
🌸
A 19. században Pisában Fibonacci szobrot állítottak és emeltek. Ma a Camposanto nyugati galériáján, a Piazza dei Miracoli történelmi temetőben található.
Számos matematikai fogalmat neveztek el Fibonacciról, mert a Fibonacci-számokhoz kapcsolódik. Ilyen például a Brahmagupta-Fibonacci azonosság,
a Fibonacci-keresési technika és a Pisano periódus.
🌸
Albrecht Dürer
🌸
https://hu.wikipedia.org/wiki/Albrecht_Dürer_(festő)
🌸
Ősei a Gyula melletti Ajtósról (Eytas) származtak,
a falu nevét mint nemesi előnevet használták („ajtósi” németül Türer).
Albrecht Dürer 1455. március 11-én, 28 évesen érkezett Nürnbergbe.
🌸
Kattints a Képekre!
🌸
Albrecht Dürer
🌸
https://hu.wikipedia.org/wiki/Albrecht_Dürer_(festő)
🌸
Ősei a Gyula melletti Ajtósról (Eytas) származtak,
a falu nevét mint nemesi előnevet használták („ajtósi” németül Türer).
Albrecht Dürer 1455. március 11-én, 28 évesen érkezett Nürnbergbe.
🌸
Kattints a Képekre!
🌸
🌸
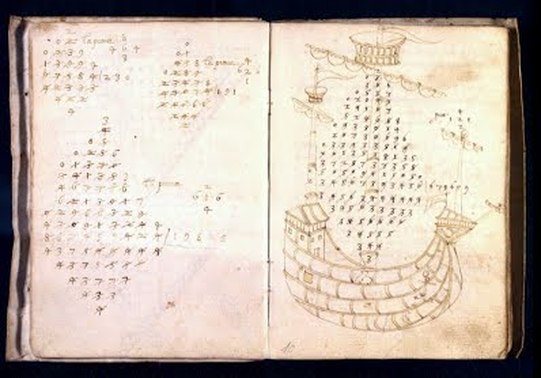
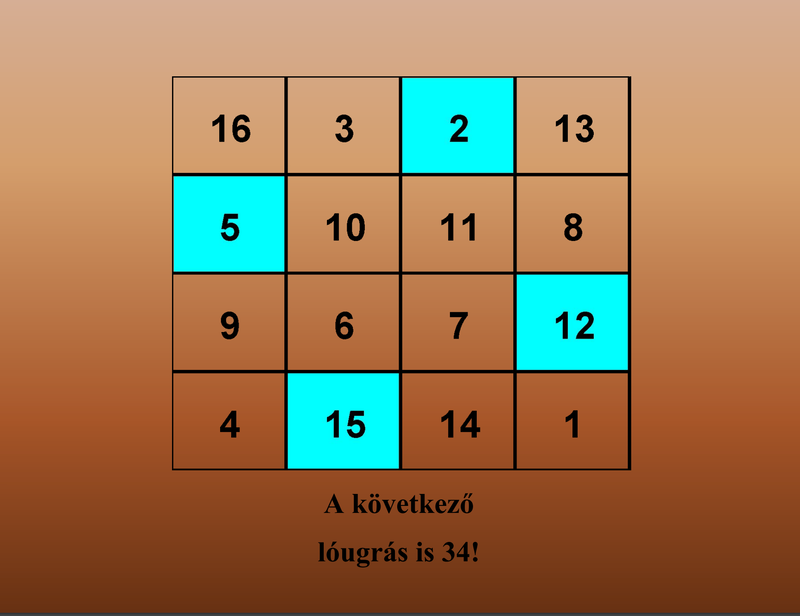
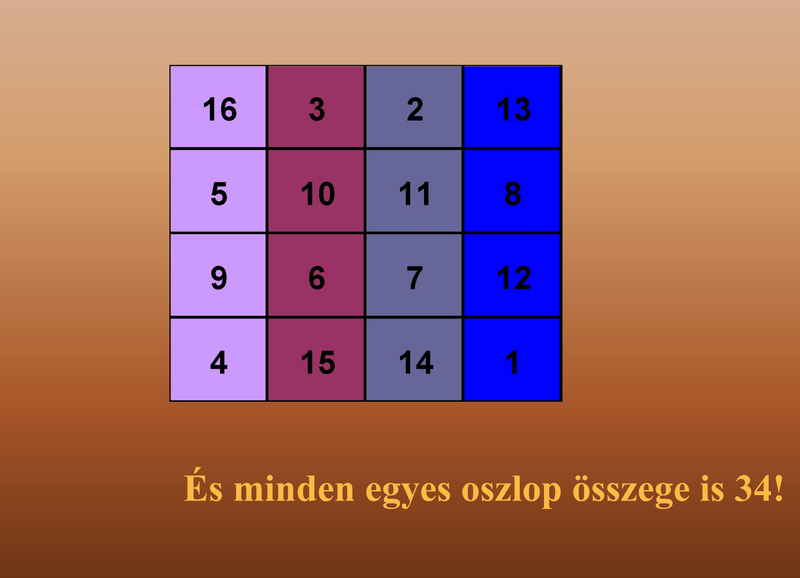
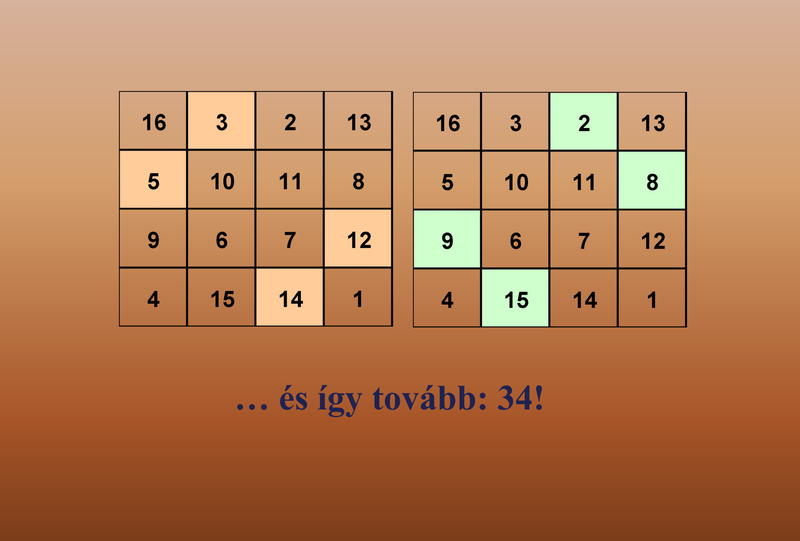
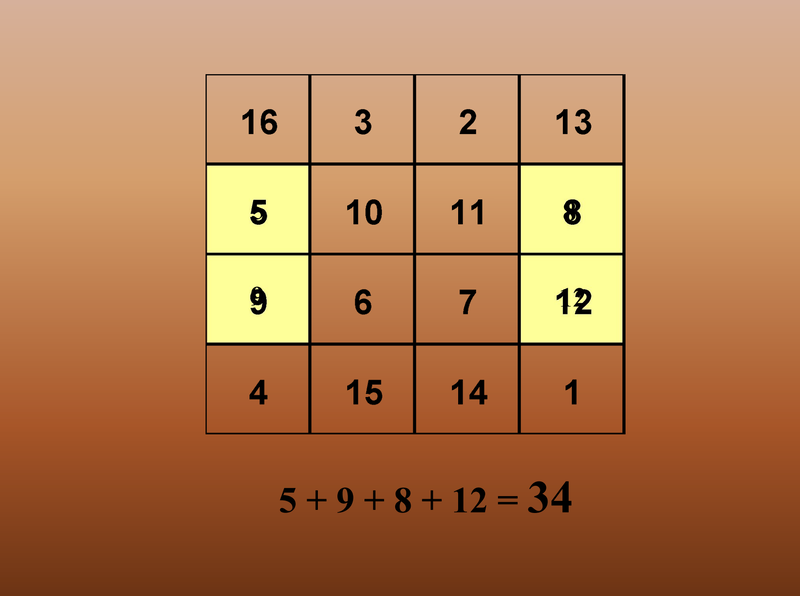
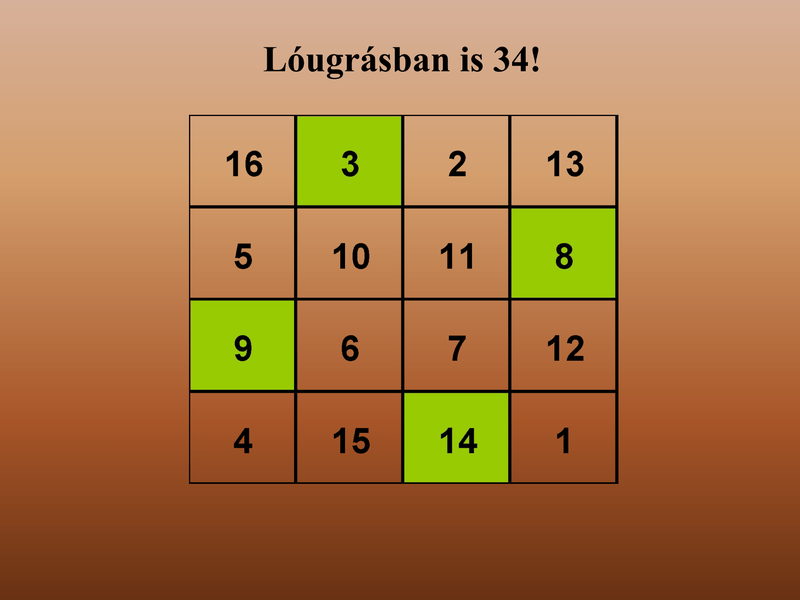
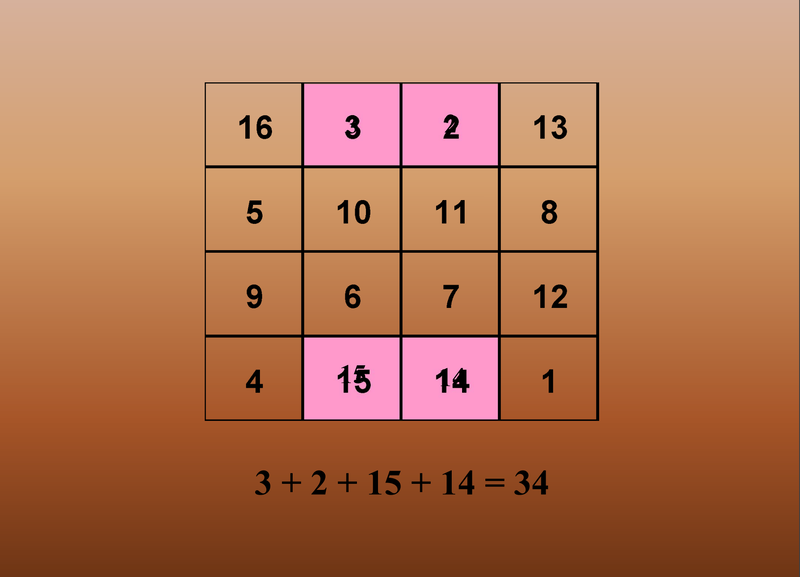
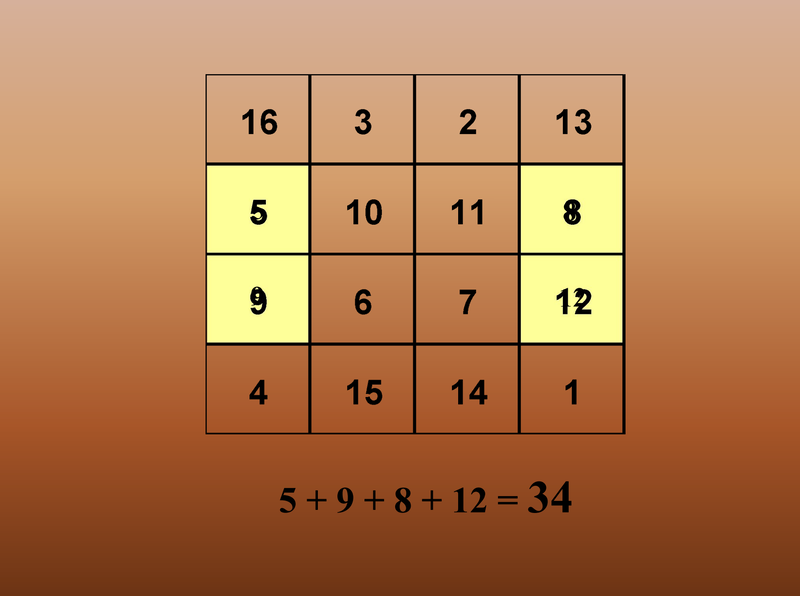
| Albrecht Dürer és a Bűvös Négyzet.pps | |
| File Size: | 2711 kb |
| File Type: | pps |
🌸
🌸
🌸
0, 1 + 1 = 2 / 1 + 2 = 3 / 2 + 3 = 5 / 3 + 5 = 8. Etc. 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
🌸
🌸
🌸
Fibonacci-vers
Egy,
egy,
kettő
és három
után jön az öt,
majd a nyolc végre rímbe köt,
s mire megjelenik a bűvös tizenhárom,
mondandómat egy huszonegy szótagszámúra nyújtott, kedves sorral zárom.
Nagymaros,
2020. június 10.
Fibonacci-vers
Egy,
egy,
kettő
és három
után jön az öt,
majd a nyolc végre rímbe köt,
s mire megjelenik a bűvös tizenhárom,
mondandómat egy huszonegy szótagszámúra nyújtott, kedves sorral zárom.
Nagymaros,
2020. június 10.
🌸
Bánlaky László
Fibonacci és a prímekszámsoros versek
FIBONACCI 1, 1+0=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13,
A 1
zöld 1
rétek 2
illatos 3
virágözönben 5
várják a szorgalmas méhek 8
látogatását, legyen jövőre is élet. 13
PRÍMEK 2, 3, 5, 7, 11, 13, s. í. t.
Édes
leányka
szíves szavára
virágcsokrot küldenék.
Helyébe hímzett keszkenőjét adja
zálogul, hogy szíve örökre legyen enyém.
Szüret után gyűrűt viszek, szülei áldását kérem én.
🌸
Az Élet Virága
Download File
http://ancientmistery.weebly.com/flower-of-life.html
https://www.ponticulus.hu/rovatok/hidverok/fibo-versek.html
🌸
Bánlaky László
Fibonacci és a prímekszámsoros versek
FIBONACCI 1, 1+0=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13,
A 1
zöld 1
rétek 2
illatos 3
virágözönben 5
várják a szorgalmas méhek 8
látogatását, legyen jövőre is élet. 13
PRÍMEK 2, 3, 5, 7, 11, 13, s. í. t.
Édes
leányka
szíves szavára
virágcsokrot küldenék.
Helyébe hímzett keszkenőjét adja
zálogul, hogy szíve örökre legyen enyém.
Szüret után gyűrűt viszek, szülei áldását kérem én.
🌸
Az Élet Virága
Download File
http://ancientmistery.weebly.com/flower-of-life.html
https://www.ponticulus.hu/rovatok/hidverok/fibo-versek.html
🌸
A számok embere
Leonardo Fibonacci nyomában
Ingyenesen letölthető PDF ... Angolul
https://www.maa.org/external_archive/devlin/Fibonacci.pdf
🌸
Leonardo Fibonacci nyomában
Ingyenesen letölthető PDF ... Angolul
https://www.maa.org/external_archive/devlin/Fibonacci.pdf
🌸